|
|
This page goes into the "nuts and bolts" of why and how an Induction Loop works and fully explains the subject using 3D trigonometry, vector diagrams and other complex terminology. Written by Leon Pieters the Managing Director of Ampetronic and someone who knows his subject inside out, from both a theoretical and practical perspective. Also has an input into setting the reference standards published by the BSI (British Standards Institute) to define how loop systems are to perform.
You will need pencil, paper and a strong Cappucino to understand this, but it IS worth studying if you want to really understand how Induction Loops work.
 |
An exploration of the basic underlying theory and practice of complex loop systems. |
| This Paper was presented to the May 1994 conference of the Institute of Sound and Communications Engineers. |
Ampetronic Ltd, Northern Road, Newark, Nottinghamshire, NG24 2ET United Kingdom Telephone: +44 (0) 1636 610062 Fax: +44 (0) 01636 610063 ampetronic.com |
| Page 1 |
 |
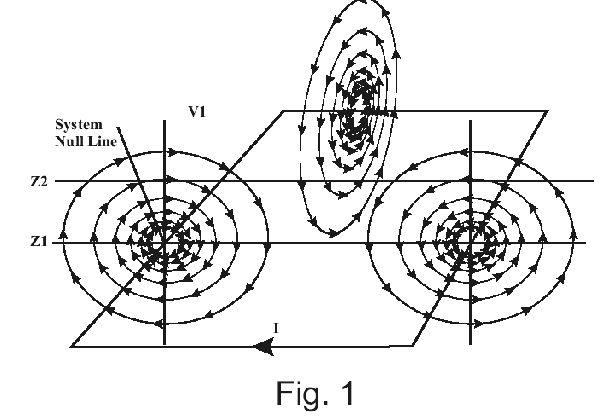
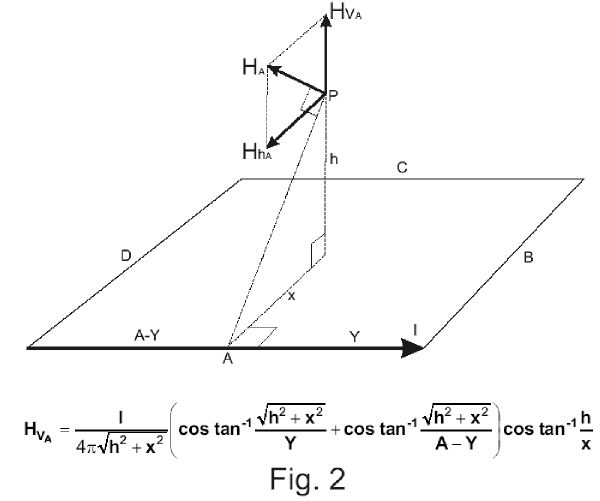
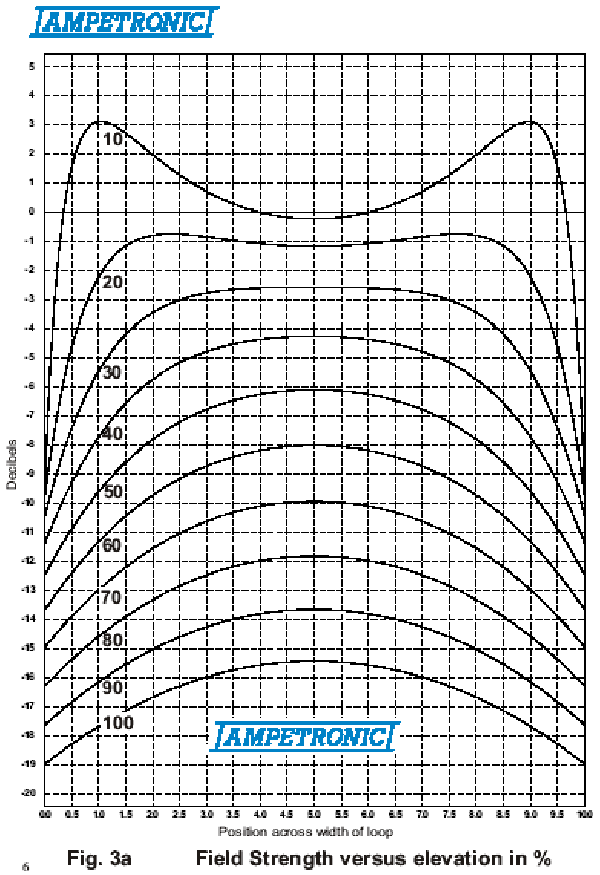
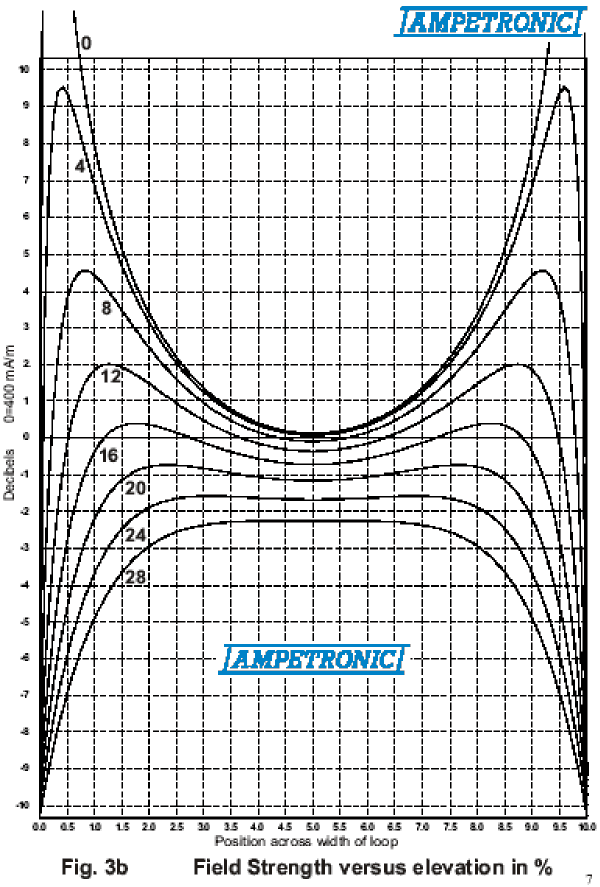
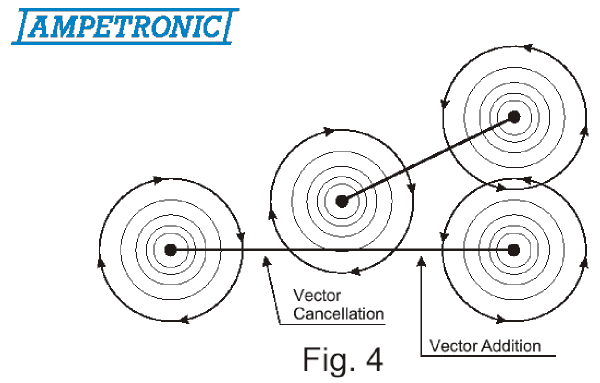
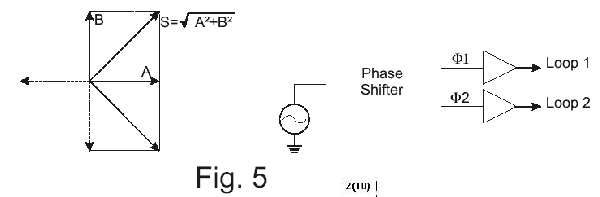
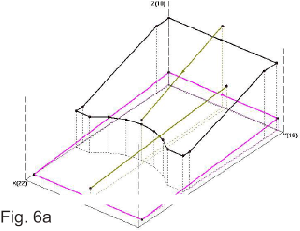
This is the fundamental formula used by Ampetronic in their computer program, where additional calculations are made for allowing wires to be positioned anywhere in space at any angle (oh, what lovely 3-D trigonometry!), current ratios between loops, phase shift with RMS summing etc. Using this tool, we can analyse the strength of the vertical magnetic component (the only one used in hearing aids, though we can look at any vector angle). If we scan along line Z1 in Fig.1, we will get a component of very high value close to the wire, and weakest in the middle. If we scan along line Z2, we will find that now we meet a "null" in the field nearly above the wire. The actual point is along a line shown as System Null Line, and this is caused by the component from the opposite wire. We have plotted the field above a 10m x 15m rectangular loop, but with the height as a percentage of the loop width. As the formula shows, only ratios matter, and this approach offers a universal solution. In Fig. 3a and Fig. 3b we have plotted against the shown percentages and this demonstrates that the worst loop position is at the hearing aid level. We normally recommend 14% as an optimum value, but as the graphs show, there is a fairly wide latitude of displacements, and of course the listening plane can be just as well above as below the loop plane.Using the vector concept, we can now begin to analyse the behaviour of complex loop patterns. A common problem is in theatres where we have loops round the stalls area and the circle (balcony) area. Fig. 4 shows the vectors due to current in both loops, which in this instance is the same phase (vertical component in the middle of each loop). Here we see that underneath the balcony, the vectors have the same orientation, and add together. However, in front of the balcony they are now opposed, i.e. trying to cancel and the field at stalls level is attenuated. This addition - subtraction problem is normally detrimental to obtaining a performance that satisfied the field strength tolerance levels of BS6083 pt. 4. An effective solution is shown in Fig. 5. The two loops are driven with signals that are phase-shifted by 90º over the entire audio band. With maximum and equal values of A and B, changing the magnitude and reversing phase, the signal sum in the receiver is the RMS sum S. This can vary by 3db when A and B are equal, and one of these components goes to null, and reverses phase. Compare this to the in-phase situation, where we can go from zero to double strength. Fig. 6a, 6b and 6c show an actual theatre situation, with a typical curved balcony at a steeper angle than the stalls area. Fig.6b is the scan from the rear to the front at stalls listening level, while Fig.6c is the same, for the balcony.
|
Four sets of curves are shown: |
|||
- both loops in phase |
Y = 0 Y = 180º |
||
For both of these situations, the current magnitude is the same (loops in series). |
||
- balcony loop at current ratio to equalise-optimise field strength Y = 180° |
||
The peaks at the rear and front are caused by the finite distance from loop plane to listening plane, which is actually too small.Another area where vector orientation matters is in crosstalk reduction between adjacent loops. Outside a loop , in the same plane, the magnetic component is mainly vertical, and positioning another loop there, fed by a weak audio signal from the main loop, does not work as the vector angles from this correction signal do not line up with the spillover component of the first loop. It should be noted that outside the loop, the components from the two sided of the loop are in opposite phase, so that a significant attenuation exists. In general, the highest peak outside a loop is about - 12db down on the signal inside the loop, and then attenuates further. |
|
Page 2 |
 |
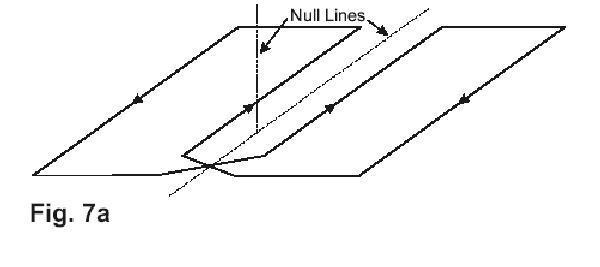
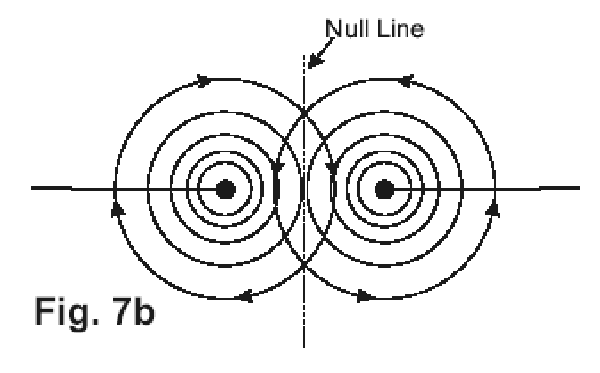
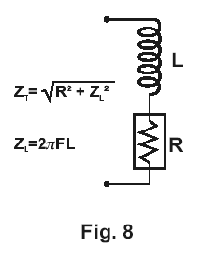
This same criteria exists where loops are stacked, and the heavily touted method of feeding a small amount of signal into a loop to cancel an external interfering signal cannot ever work at the crosstalk levels of -40db relative to normal signal used by Ampetronic in the design of low-spill systems.Another further area of concern is the installation of loops in a mosque, where the worshipper bends over until the head is touching the floor, and the hearing aid axis is nearly horizontal. Special solutions are needed for this. In lecture theatres and conference rooms similar considerations can apply as the listener may bend the head substantially while making notes, and the local magnetic orientation needs checking to prevent undesirable null areas. An analysis of magnetic vectors also shows that in multi-loop systems, crossover areas, etc. as shown in Fig. 7a, there is no need to keep the conductors close together. A magnetic "null" (vertical component) exists on the centre line, as is shown in Fig. 7b. This method of creating a spatial null away from the cable can sometimes be very desirable in the design of dedicated systems. 2. Amplifier Power and Loop Specification A significant area of misapprehension exists on the specification of the loop driver and the cable to use. Despite the design of specialised current driving amplifiers, design to drive single-turn loops, we still find in various designs methodologies (such as published in “Public Address” recently coming from the Millbank stable) references to using multi-turn loops. A length of wire positioned as a loop looks like a normal R-L network as shown in Fig. 8. The impedance rises by 3db at the frequency where R=|Z |. This also means that when driven by a normal (voltage) amplifier, this will be the -3db response frequency in the absence of specialised correction.
|
| Cable Section in mm² |
Single Turn Loop |
2 - Turn Loop |
3 - Turn Loop |
| 0.50 | 2864 | 1432 | 954 |
| 0.75 | 1910 | 955 | 637 |
| 1.00 | 1432 | 716 | 477 |
| 1.50 | 955 | 477 | 318 |
| 2.50 | 573 | 286 | 191 |
| Cable Section AWG |
Single Turn Loop |
2 - Turn Loop |
3 - Turn Loop |
| 22 | 4052 | 2026 | 1350 |
| 20 | 2548 | 1274 | 849 |
| 18 | 1772 | 884 | 591 |
| 16 | 1091 | 545 | 364 |
| 14 | 697 | 346 | 231 |
| 12 | 436 | 218 | 145 |
| 10 | 275 | 137 | 92 |
| Table 1: -3db frequency in Hz versus copper size for loop cables. |
| Page 3 |
 |
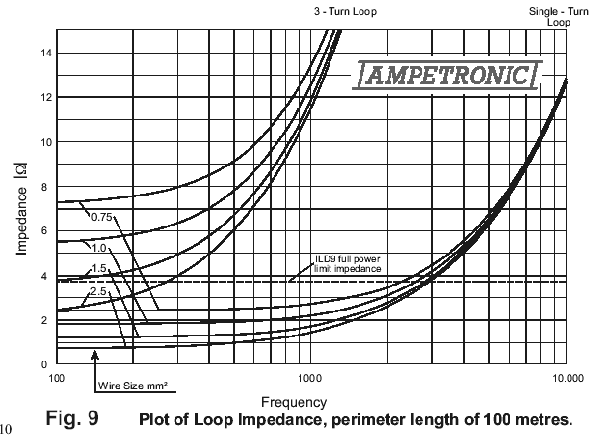
It is accepted that the inductance of wire is very nearly 2µH/metre, for single cable in space. This allows us to establish a frequency for each cable size where this -3db point falls. The data in table 1 is given for single, two and three-turn loops. As the inductance is little affected by the loop size, the figures can be used with some measure of accuracy.The reduction in corner frequency is due to the fundamental fact that while resistance increases linearly with the number of turns, the inductance is increased by the square of the turns number. Hence, for a 3-turn loop, R increases 3 fold, Z increases 9 fold, hence the corner frequency is reduced by a factor of 3. This is shown even more clearly in Fig. 9, which shows the impedance of a 20m x 30m loop (100m perimeter) against frequency for different wire sizes in single and 3-turn configurations. All amplifiers have a limiting output voltage, and operation into the clipping area generates RFI which will become illegal. At the output current needed, this gives a limiting impedance for the amplifier. Analysis of the power distribution of speech indicates that the amplifier must be capable of supplying the loop with the full required current at all frequencies up to at least 1.5KHz, beyond which the drive capability can be allowed to drop at 6db/octave . Note that this is not the same as frequency response, which I believe should be measured 20db below maximum current, to allow for the peak limitation effect, and any signal processing to eliminate clipping. Obtaining the loop impedance at 1.5KHz, and knowing the amplifier limiting impedance permits us to estimate whether the loop - amplifier combination is acceptable. Regrettably, most manufacturers do not publish the peak output voltage. Fig.9 indicates the maximum full-power impedance for the ILD9 loop driver, and it can be seen that this amplifier has no difficulty satisfying the frequency requirements on this size loop. We do know of several instances where this has been impossible, mainly because long, narrow loops can require a current well inside the capability of the amplifier, yet the total cable length is such that the circuit impedance is too high. A further aspect of this is the need to choose a copper resistance which is less than this maximum, so that there is headroom for the inductive component. Several suppliers seem to ignore this vital aspect. Fig. 9 demonstrates also clearly the near-impossibility of driving multi-turn loops in current mode. In voltage mode, the frequency correction needed to meet the frequency response requirements of BS6083 pt.4 is virtually non-practical, while also needing a very powerful amplifier. This is due to the need for full current capability when driving impedances of greater than 15. This equates to a high power into a reactive load, for which normal amplifiers are not designed. This paper has addressed two major areas of concern in AFILS, but there are many others that need attention and guidance. Regrettably, very little of this exists anywhere in print. Page 4 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
© 1994-2026 DTSystems. All Rights Reserved. |
|
Home | Prices | Contact | Terms | Site Map | Audio Induction Loop Theory |